Iterated Prisoner's Dilemma with Rust
The only winning move is...

Prisoner's Dilemma has been used to model situations from business deals to nuclear policy[1]. The unfortunate finding is that in a single round game, it's strategically optimal for both players to defect, giving out a lower payout than if they both simply cooperated.
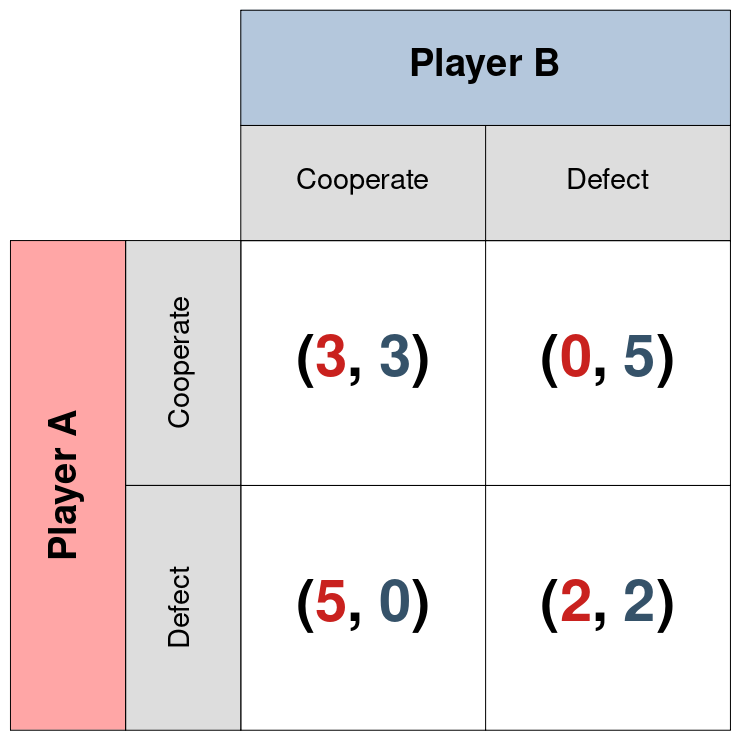
In the diagram below, player 1's moves are on the rows and player 2's moves are on the columns. Player 1's and 2's payoffs are first and second entries on the tuples corresponding to the pair of strategies played.
Nash Equilibrium and Best Response
This result comes from Nash Equilibrium, which defines a particular set of strategies. Simply put, a set of actions is a Nash Equilibrium if neither player can choose a different action and do better without the other players also changing their moves[2].
Given the payoff matrices for Prisoner's Dilemma, this is fairly evidently the case for the pair of actions (Defect, Defect). Given that player 1 plays defect, player 2 can either achieve a payoff of 2 with defect, or a payoff of 0 with cooperate. Alternatively, given that player 1 cooperates, player 2 can either achieve a payoff of 3 by cooperating, or a payoff of 5 for defecting. In both situations, the best thing to do for a player is to defect, and by symmetry this holds for player 1 as well.
This structure of: given player 1's move, what's best for player 2? forms a best response to player 1's move. By finding both players best responses to the other's range of strategies, the pure strategy Nash equilibria can be found. The strategy here is called pure because it does not allow for randomized choice by the players. There are ways to find these Nash equilibria for mixed (randomized) strategies, but that's beyond the scope of this posting.
Repeated Games
So defection is optimal when playing this game once, but what about repeated plays with the same partner? The bedrock of civilization is the ability to play long term games with other people. When someone rips you off, you don't do business with them. When they deliver on expectations, the relationship is likely to continue. Iterated Prisoner's Dilemma takes the already displayed form of the game and has the players play multiple rounds.
The Axelrod tournaments are famous for studying arrangement[3]. In these tournaments, Axelrod requested submissions for programs to play each other. This was done in a round robin setup so every strategy submitted played against everything else. At the end the strategy had its points summed up to rank their performance.
The winner of both round 1 and round 2 of the tournament was called Tit-for-Tat (or kontrageben in German). The strategy is to initially cooperate and from then on to do whatever the opponent did last.
Axelrod points out a few attributes that go into making it such a strong strategy but is (rightly) hesitant to call it optimal. Tit-for-Tat is nice, easily provoked, and forgiving. By nice it means that the strategy initially cooperates. Easily provoked meaning that when defection occurs, it is willing to defect as well. In this case, whenever the opponent defects, it defects on the next move. Lastly, it is forgiving in that when the opponent cooperates after defecting, it goes back to cooperating.
This strategy is interesting as it models the ability for players to build trust between one another in a way that's reliant on the structure of the game. It suggests at selfish behavior that looks a lot like altruism.
Some other strategies worth mentioning are the naive Nash equilibrium of always defecting, and grim trigger. Grim trigger works by cooperating until the opponent defects, and thereafter defecting in perpetuity. One last strategy I'll explore here is random defection with some probability.
Similarly to the Axelrod paper, I'll have every strategy allocated to two players which all play each other for five rounds of lengths specified by the paper. Then I'll sum up the total scores for each players and see how they did. Because this is deterministic, playing for the 5 rounds is unnecessary but is in keeping with Axelrod and will generalize nicely to some things I'd like to try later.
Running all that, we get out the following:
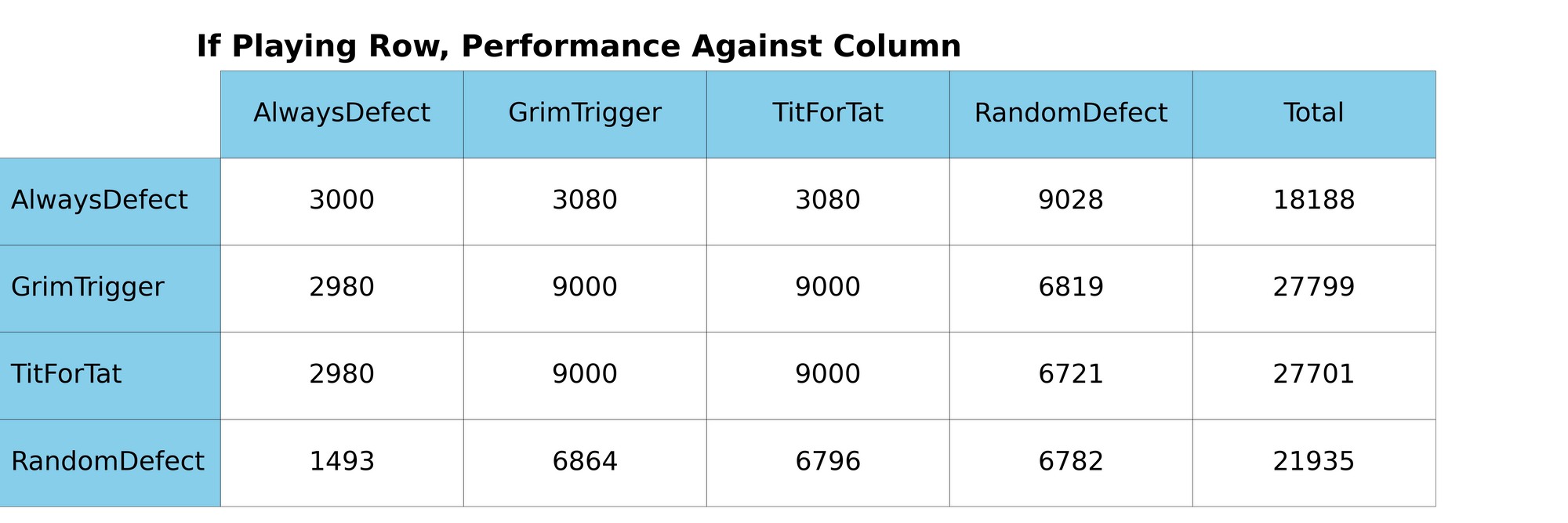
Here we see that apart from differences in the random strategy, Grim Trigger and Tit for Tat give better performance than sticking with the naive strategy of consistent defection when viewed over strategies.
It can be expected through that when intermediate strategies that may forgive after multiple rounds of cooperation are included, Grim Trigger would be unable to forgive, whereas Tit for Tat may. In this setup, Tit for Tat can be expected to outperform Grim Trigger.
As an aside, it may be reasonable for a player to model the present over the future[2]. The degree to which this is the case is referred to as time preference. Time preference has significant implications as a perfectly shortsighted player would always defect no matter what rather than cooperate somewhat over time. One way of modelling this is discussed in Osborne and for various values of a parameter meant to encode time preference, the values of that parameter strategies are optimal are found.
Performance Against Random Defection
Another thing worth doing is to model their behavior against random defection. With some probability p of defecting, the scores for each strategy are shown below.
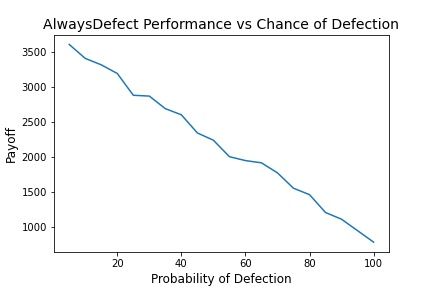
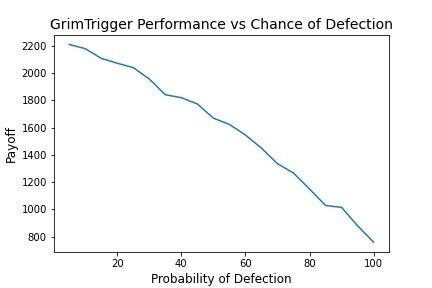
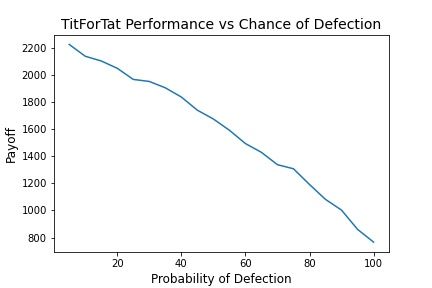
We see overall we see that consistent defection achieves the highest payoff over all values. This is interesting as it seems to say that in an absence of another truly strategic player, the best way to play is to stick with a Nash Equilibrium. I half expect that statement is a theorem somewhere that I simply haven't run across yet but there it is.
Grim Trigger and Tit for Tat perform similarly in that defection has no bearing on the opponent's future performance. Grim Trigger may win if the opponent cooperates. The situation is the same for Tit for Tat. Grim Trigger makes up for the necessary loss of cooperation though (Defect, Cooperate) wins and Tit for Tat makes up for it in the possibility of (Cooperate, Cooperate). Result being a wash.
Next Steps
All in all this is a first pass at playing with Iterated Prisoner's Dilemma. The next step is to set this game structure up with populations that die off and spawn additional instances of the winners over rounds. This was done in Axelrod as well. Following on from that, I'd like to set up an evolutionary algorithm to solve for better performance over this iterated setup. Those bits of progress will be the subject of the next posting.
Materials
I've used this project as an opportunity to learn Rust. The simulations themselves were written in Rust. This was set up with multithreading to be able to handle each player's game in parallel. I expect this will prove beneficial in the future as I anticipate running over a much wider variety of conditions with more players. In this setup it stores off all the data in jsons.
Then all the data are loaded up in python for analysis. I'm okay with this being slow for now. As time goes on though, it may become necessary to evaluate some of the metrics on the fly between rounds in an evolutionary algorithm.
Sources
[1] Strategy of Conflict by Thomas Schelling
[2] Prisoner's Dilemma from Wikipedia
[3] An Introduction to Game Theory by Martin J. Osborne
[4] More Effective Choice in the Prisoner's Dilemma by Robert Axelrod